よくここまで頑張りました!
音楽をやってみたい!と意気込んで『学習カテゴリ:初歩の初歩』から始めてみたものの、あまり楽しく無かったという方も少なくなかったのではないでしょうか?
しかし音楽を始める上で絶対に必要な知識です。確実に身に着けておいて下さい。
基本的な知識はあなたが音楽をする上で必ず助けになります。
実は『学習カテゴリ:初歩の初歩~初歩』までは『楽典』という分野で、
『音楽理論』という領域にまで達していません。その『音楽理論』を学ぶ為に必要不可欠な下知識なのです。
『楽典』という言葉は音楽に接することの無い人にとっては全く聞きなれない言葉で、この言葉を使うと『勉強感』が出すぎてしまい、学ぶ意欲を削いでしまうことがあるため、敢えてこの言葉はここまで使ってきませんでした。
しかしながら、ここからは少し音楽的なことの学習になっていくので、徐々に理解していくことに対して楽しみを味わうことが出来ると思うので、『楽典』というものが『音楽理論』を学ぶ為に必要な下知識であるということを知ってもらうために紹介しました。
それでは『学習カテゴリ:初歩』を学んでいきましょう!!
音程・度数
音程
音程という言葉は1つの音に対して使うものではなく、2音間の音の高さの違いに対する名称のことです。
音程の響きを理解し、そのしくみを知る事は音楽理論を学ぶ上でも最大級の重要項です。
幹音
幹音とは、(#)や(♭)等の半音階的変化を受けない音のことです。
つまりピアノの白鍵部分の音に相当し、自然音とも呼ばれます。
度数
音程は全て度数で表されます。
度数とは2音間に含まれる幹音の数を示すもので、度数を計算する時は(#)や(♭)等の変化記号を無視して考えます。
つまり、白鍵盤のみで計算をすれば良いことになります。
例えば下の画像の様に『C(ド)』と『E(ミ)』の場合、白鍵盤を数えると幹音が3つ含まれる為3度の関係となります。
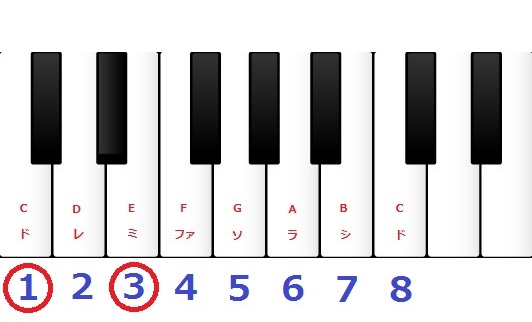
また、『E(ミ)』と『G(ソ)』でも下の画像の様に幹音が3つ含まれるため3度の関係となります。
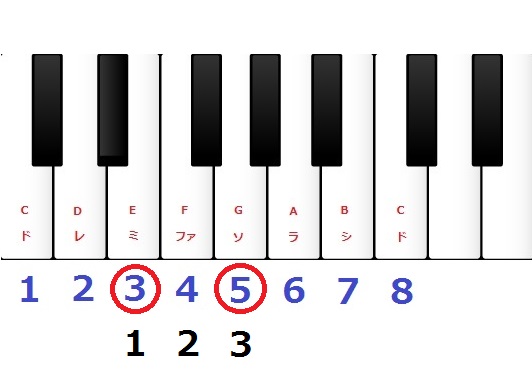
下の画像のように『D#(レ#)』と『F(ファ)』でも、度数を考えるときは変化記号を無視して良いので白鍵盤を数え、幹音が3つ含まれるため3度の関係であることが分かります。
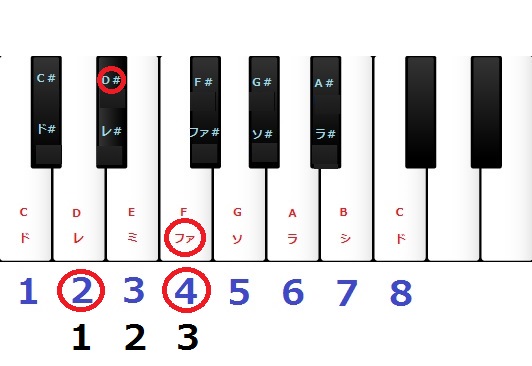
以上を踏まえ、下に『C(ド)』の音を基音にした度数を見てみましょう。
『C(ド)』と『C(ド)』

『C(ド)』と『D(レ)』

『C(ド)』と『E(ミ)』

『C(ド)』と『F(ファ)』

『C(ド)』と『G(ソ)』

『C(ド)』と『A(ラ)』

『C(ド)』と『B(シ)』

『C#(ド#)』と『A(ラ♭)』

オクターブ・複音程
オクターブ
オクターブとは、ある音階を基準とした、音の高さの異なる同名の音階までの音程のことを言います。例えば『C(ド)』の音階を鳴らしたとき、1つ高い(低い)『C(ド)』までの音程が1オクターブとなります。2~3つ高い(低い)音程は2オクターブ、3オクターブなどと呼びます。
度数の関係は次の様になります。
『C(ド)』と『C(ド)』

複音程
8度までの音程は短音程、オクターブを越える音程のは複音程と呼びます。
例えば下の画像の様に1オクターブ以上はなれた音程には2種類の呼び方があります。
『C(ド)』と『E(ミ)』

